• ingenieria-de-control
• proyectos

Modelado de un edificio I

March 10, 2013

A través de este post de Mimbrea, llegué a una hoja de cálculo bastante cerrada donde se exponían los conceptos de amortiguación térmica y desfase térmico de las construcciones y mediante la misma se podía calcular esos datos. En el mismo documento se afirma que lo óptimo es obtener un desfase térmico cercano a las 12 horas.

A raíz de la explicación que daba, me surgieron ciertas dudas sobre si era posible conseguir desfasar la temperatura 12 horas. Para comprobarlo voy a intentar modelar de la forma más sencilla posible un edificio, no entraré en detalle, simplemente obtendré la estructura, los valores de los coeficientes se pueden obtener por identificación, si la cosa va bien, el siguiente paso será hacer una identificación de un edificio real y extraer de ahí datos útiles.

Para simplificar al máximo el modelo vamos a imaginar que tenemos una construcción cerrada, con todos los muros iguales y de algún material desconocido, ni puertas ni ventanas, una caja negra que vamos a destripar, para convertirla en una caja gris.

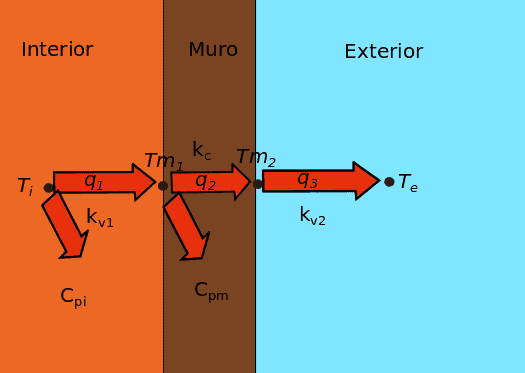
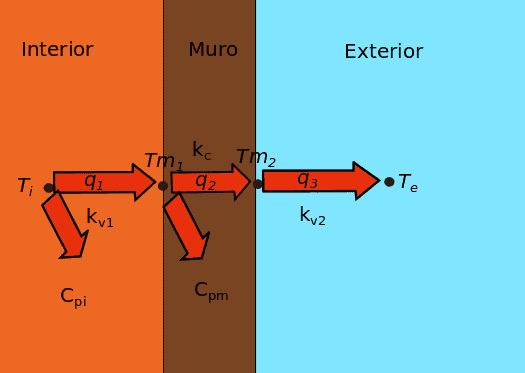
Lo primero es conocer las variables del modelo, en el siguiente esquema las escribiremos en cursiva, como sabemos, el calor se transmite de 3 formas, convección, conducción y radiación, por el momento nos olvidaremos de la radiación, con lo que nos quedan convección para transmisión en fluidos y conducción para los sólidos. Nos interesan por lo tanto las temperaturas de los fluidos, aire interior(ti) y exterior(te) y la de los sólidos, los muros por la parte interior(tm1) y exterior(tm2). Representaremos las temperaturas con un punto negro. Las siguientes variables a tener en cuenta son los flujos de calor, representados como una flecha roja, son q1, q2 y q3.

Las constantes no nos interesan tanto pero pondremos en el esquema las que dependen del material utilizado, sin cursiva.

Empezaremos con una ecuación sencillita, como sabemos que la energía se conserva tenemos que:

(1) $q_{2}-q_{3}=0$

Luego ponemos las ecuaciones de la convección, el nuevo termino que nos encontramos es A, que corresponde al área del muro, pero no nos va a hacer falta por ahora:

(2) $q_{1}=k_{v1}A(T_{m1}-T_i)$

(3) $q_{3}=k_{v2}A(T_e-T_{m2})$

Lo siguiente es la que afecta a la conducción en el muro:

(4) $q_{2}=k_{c}A(T_{m2}-T_{m1})$

Después pasamos a las ecuaciones del calor especifico de los cuerpos, m representa la masa del aire:

(5) $q{1}=C_{pi}m\frac{dT_{i}}{dt}$

(6) $q_{2}-q_{1}=C_{pm}m\frac{dT_{m1}}{dt}$

Con estas 6 ecuaciones ya tenemos definido el modelo del edificio, puesto que tenemos 2 variables de estado Ti y Tm1, 1 variable de entrada Te y 6 variables auxiliares, el resto. Obtenemos de esta forma un modelo de 2º orden con un bastantes constantes ligadas entre ellas. En próximo post de esta serie veremos como extraer información del modelo y como identificar los parámetros de ese modelo sin necesidad de conocer todas las constantes.